- Закон двойного отрицания (двойное отрицание исключает отрицание):
А = 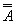 . . - Переместительный (коммутативный) закон:
Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания. - Сочетательный (ассоциативный) закон:
При одинаковых знаках скобки можно ставить произвольно или вообще опускать. - Распределительный (дистрибутивный) закон:
Закон определяет правило выноса общего высказывания за скобку. - Закон общей инверсии (законы де Моргана):
- Закон идемпотентности (от латинских слов idem — тот же самый и potens — сильный; дословно — равносильный):
Закон означает отсутствие показателей степени. - Законы исключения констант:
для логического сложения: А Ú 1 = 1, А Ú 0 = A; для логического умножения: A & 1 = A, A & 0 = 0.
- Закон противоречия:
A & 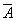 = 0. = 0.
Невозможно, чтобы противоречащие высказывания были одновременно истинными. - Закон исключения третьего:
A Ú 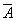 = 1. = 1.
Из двух противоречащих высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано. - Закон поглощения:
Знание законов логики позволяет проверять правильность рассуждений и доказательств. Основываясь на законах, можно выполнять упрощение сложных логических выражений. Такой процесс замены сложной логической функции более простой, но равносильной ей, называется минимизацией функции. Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), другие - основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.). Нарушения законов логики приводят к логическим ошибкам и вытекающим из них противоречиям. Упрощение формул. Пример 1. Упростить формулу (А Ú В) & (А Ú С). Решение: - Раскроем скобки: (А Ú В) & (А Ú С) = A & A Ú A & C Ú B & A Ú B & C;
- По закону идемпотентности A & A =A, следовательно,
A & A Ú A & C Ú B & A Ú B & C = A Ú A & C Ú B & A Ú B & C; - В высказываниях А и А & C вынесем за скобки А и используя свойство А + 1= 1, получим
A Ú A & C Ú B & A Ú B & C = A & (1 Ú C) Ú B & A Ú B & C = A Ú B & A Ú B & C; - Аналогично предыдущему пункту вынесем за скобки высказывание А.
A Ú B & A Ú B & C = A & (1 Ú B) Ú B & C = A Ú B & C.
Таким образом, мы доказали закон дистрибутивности. Всякую формулу можно преобразовать так, что в ней не будет отрицаний сложных высказываний - все отрицания будут применяться только к простым высказываниям. Пример 2. Упростить выражения 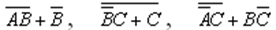 так, чтобы в полученных формулах не содержалось отрицания сложных высказываний. так, чтобы в полученных формулах не содержалось отрицания сложных высказываний. Решение:
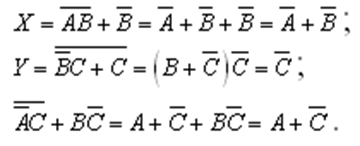
Источник: http://qo.do.am | 