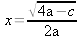1. Логические величины, операции, выражения. Логические выражения в качестве условий в ветвящихся и циклических алгоритмах.

Для того чтобы понять работу ветвящихся и циклических алгоритмов, рассмотрим понятие логического выражения.

В некоторых случаях выбор варианта действий в программе должен зависеть от того, как соотносятся между собой значения каких-то переменных.

Например, расчёт корней квадратного уравнения производится по-разному в зависимости от дискриминанта (вспомните математику).

В результате сравнения значений двух выражений возможны два варианта ответа: сравнение истинно или ложно?

Например:

2+3 > 3+1 - да (истинно)

0 < -5 - нет (ложно)

Выражения такого вида мы будем называть логическими выражениями.

Логическое выражение, подобно математическому выражению, выполняется (вычисляется), но в результате получается не число, а логическое значение: истина (true) или ложь (false). Логическая величина – это всегда ответ на вопрос, истинно ли данное высказывание.

Нам известны шесть операций сравнения:

С помощью этих операций мы будем составлять логические выражения. Причём в выражениях не обязательно присутствуют только константы, но и переменные.

5 > 3

a < b

c <> 7

Как выполняются операции отношения для числовых величин понятно из математики. Как же сравниваются символьные величины? Отношение «равно» истинно для двух символьных величин, если их длинны одинаковы и все соответствующие символы совпадают. Следует учитывать, что пробел тоже символ.

Символьные величины можно сопоставлять и в отношениях >, <, >=, <=. Здесь упорядоченность слов (последовательности символов) определяется по алфавитному принципу.

«кот» = «кот»

«кот» < «лис»

«кот» > «дом»

Выражение, состоящее из одной логической величины или одного отношения, будем называть простым логическим выражением.

Часто встречаются задачи, в которых используются не отдельные условия, а совокупность связанных между собой условий (отношений). Например, в магазине вам нужно выбрать туфли, размер которых r = 45, цвет color = белый, цена price не более 400руб.

Другой пример: школьник выяснил, что сможет купить шоколадку, если она стоит 3руб. или 3руб. 50коп.

В первом примере мы имеем дело с тремя отношениями, связанными между собой союзом "и" и частицей "не", во втором - с двумя отношениями, связанными союзом "или". Подобные условия назовём составными, и для их обозначения в алгоритме договоримся использовать союзы "и", "или", "не", которые будем рассматривать как знаки логических операций, позволяющих из простых условий создавать составные, подобно тому, как из простых переменных и констант с помощью знаков +, - и т. д. можно создавать алгебраические выражения.

Так условия наших примеров в алгоритме могут выглядеть таким образом:

первое: (r = 45) и (color = белый) и (не (price>400))

второе: (цена=3) или (цена=3.5)

Выражение, содержащее логические операции, будем называть сложным логическим выражением.

Объединение двух (или нескольких) высказываний в одно с помощью союза «и» называется операцией логического умножения иликонъюнкцией.

В результате логического умножения (конъюнкции) получается истина, если истинны все логические выражения.

Объединение двух (или нескольких) высказываний с по мощью союза «или» называется операцией логического сложения или дизъюнкцией.

В результате логического сложения (дизъюнкции) получается истина, если истинно хотя бы одно логическое выражения.

Присоединение частицы «не» к высказыванию называется операцией логического отрицания или инверсией.

Отрицание изменяет значение логической величины на противоположное: не истина = ложь; не ложь = истина.

Если в сложном логическом выражении имеется несколько логических операций, то возникает вопрос, в каком порядке их выполнит компьютер. По убыванию старшинства логические операции располагаются в таком порядке:

1. отрицание (не);

2. конъюнкция (и);

3. дизъюнкция (или).

В логических выражениях можно использовать круглые скобки. Так же как и в математических формулах, скобки влияют на последовательность выполнения операций. Если нет скобок, то операции выполняются в порядке их старшинства.

Пример. Пусть a, b, c – логические величины, которые имеют следующие значения: a = истина, b = ложь, c = истина. Необходимо определить результаты вычисления следующих логических выражений:

1. a и b

2. a или b

3. не a или b

4. a и b или c

5. a или b и c

6. не a или b и c

7. (a или b) и (с или b)

8. не (a или b) и (с или b)

9. не ( a и b и c)

Получим в результате:

1. ложь

2. истина

3. ложь

4. истина

5. истина

6. ложь

7. истина

8. ложь

9. истина.

Пример. Составить алгоритм для вычисления:

Компьютер сначала проверит условие (4*а – с >=0) и (а<>0) и если оно окажется истинно, то вычислить x, иначе выведет сообщение «нет решения».

Пример. Составить алгоритм для вычисления суммы всех чисел от 1 до n.

До тех пор пока условие x<n будет истинно компьютер будет выполнять тело цикла – вычислять очередную сумму и увеличивать x на единицу.